Compiler Optimization (4): Induction Variables
0. Basic Knowledge
0.1 Loop
Definition
A loop, or a natural loop in LLVM, is a set of nodes (L) from the control-flow graph (CFG) with the following properties [1] [2]:
- There is a single entry node (called a header), which controls all nodes in the loop.
- There is a backedge that enters the loop header.
Terms
- Entering block: A non-loop node that has an edge connected to the loop. If there is only one entering block and its only edge is connected to the header, it is also called the preheader. The peheader that functions as a non-loop node dominates the entire loop.
- Latch: A loop node that has an edge to the header.
- Backedge: An edge from the latch to the header.
- Exiting edge: An edge from inside the loop to a node outside the loop. The start node of the edge is called an exiting block, and the end node is called an exit block.
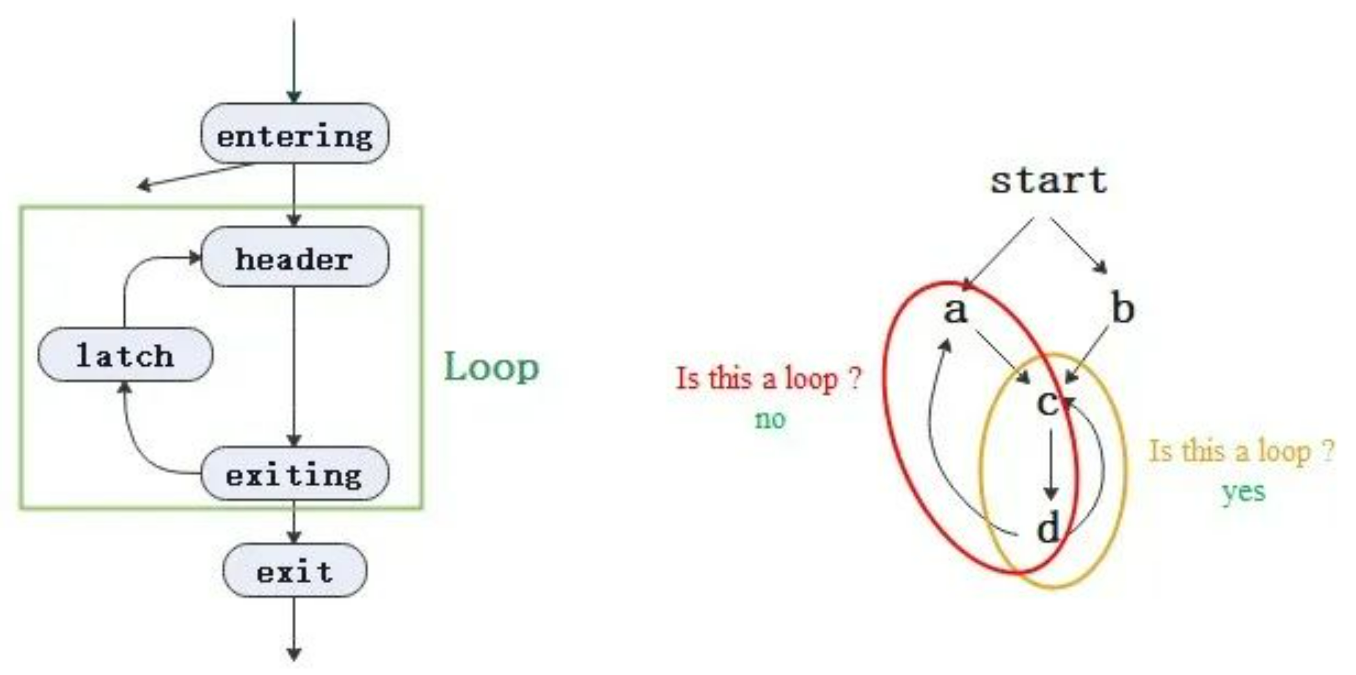
In the figure on the right, the yellow area is a loop; the red area is not, because it has two entry nodes a and c.
0.2 Scalar Evolution (SCEV)
Definition
SCEV is an optimization pass used by the compiler to analyze variables (usually integers). It is mainly used to analyze how variables in a loop are updated and then optimize variables based on the analysis.
**Chains of Recurrences **(CR)
As shown in the following figure, the start value of the induction variable var in the loop is start, the iteration mode is ϕ, and the step is step.
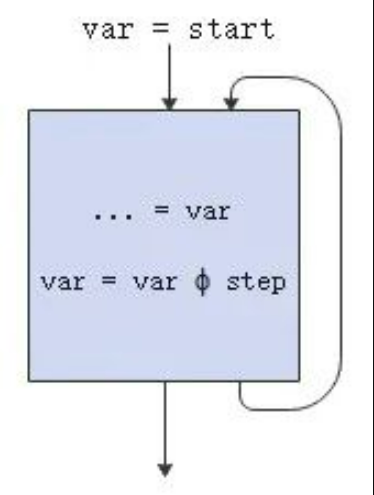
Its CR is as follows:
var = {start, ϕ , step}
// ϕ∈{+,∗}
// start: starting value
// step: step in each iterationExample:
int m = 0;
for (int i = 0; i < n; i++) {
m = m + n;
*res = m;
}In the example, m = {0, +, n} is the CR.
1. Induction Variable
1.1 Definition
for (i = 0; i < 10; ++i) {
j = 17 * i;
}1.2 Benefits
The advantages of induction variable optimization include but are not limited to the following:
- The original calculation method could be replaced with a simpler instruction. For example, the multiplication in the code above can be replaced with an addition at a lower cost.
j = -17;
for (i = 0; i < 10; ++i) {
j = j + 17;
}- The number of induction variables is decreased to reduce the pressure on the register.
extern int sum;
int foo(int n) {
int i, j;
j = 5;
for (i = 0; i < n; ++i) {
j += 2;
sum += j;
}
return sum;
}The loop now has two induction variables: i and j. After one variable is used to express the other, the following information is displayed:
extern int sum;
int foo(int n) {
int i;
for (i = 0; i < n; ++i) {
sum += 5 + 2 * (i + 1);
}
return sum;
}- Induction variable substitution makes the relationship between variables and loop indexes clear, facilitating other optimization analyses, such as dependency analysis. In the following example, c is expressed as a function of a loop index.
int c, i;
c = 10;
for (i = 0; i < 10; i++) {
c = c + 5; // c is incremented by 5 for each loop iteration
}Then:
int c, i;
c = 10;
for (i = 0; i < 10; i++) {
c = 10 + 5 * (i + 1); // c is explicitly expressed as a function of loop index
}2. Practices
2.1 Compilation Options
| Compiler | Option |
|---|---|
| gcc | fivopt |
| BiSheng Compiler | indvars |
2.2 Optimization Case
The induction variable optimization (ivs) is in llvm\lib\Transforms\Scalar\IndVarSimplify.cpp. Let's look at the optimization process of the BiSheng Compiler through a use case. As shown in the following figure, assume that the upper func part is the code to be optimized, and the lower func part is the expected result.

Its IR case test.ll is as follows:

The compilation command is as follows:
opt test.ll -indvars -SIn the current example, the header, latch, and exiting block are the same basic block (BB), that is, bb5.

Step 1: Traverse the source of the operand of the phi node in ExitBlock of the loop based on the def-use relationship, calculate the final value, replace the operand, and then replace the phi node.
In the example, the only operand for calculating %tmp2.lcssa is %tmp2 = add nuw nsw i32 %i.01.0, 3 , and the loop where the expression is located is bb5. In this case, the CR of %tmp2 is as follows:
%tmp2 = {3,+,3}<nuw><nsw><%bb5>The maximum number of times that the current loop can be repeated before it exits is 199999, which means %tmp2=add(3, mul(3,199999))=600000. The current substitution cost is low (the cost calculation varies according to the architecture). Replace the value in the user of the phi node. The optimization results are as follows:
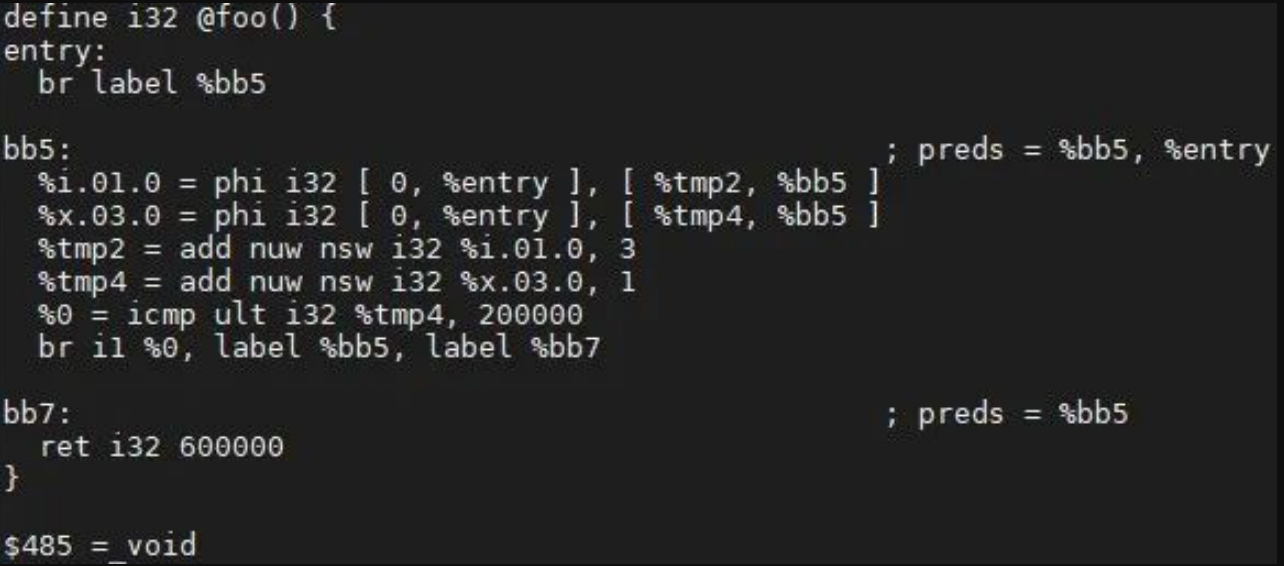
Step 2: Traverse the ExitingBlock, calculate the jump condition, and delete the corresponding instruction according to the def-use relationship. In the example, %0 of br i1 %0, label %bb5, label %bb7 is false. After the jump instruction is replaced, %0 = icmp ult i32 %tmp4, 200000 does not have a user, so it is added to dead instructions. The optimization results are as follows:
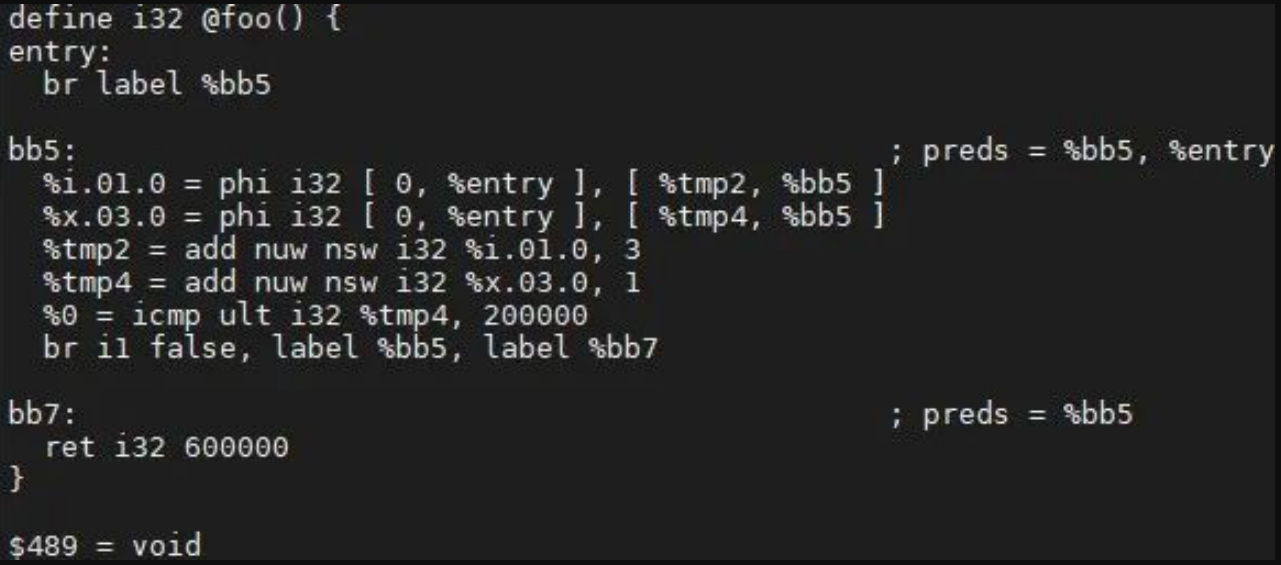
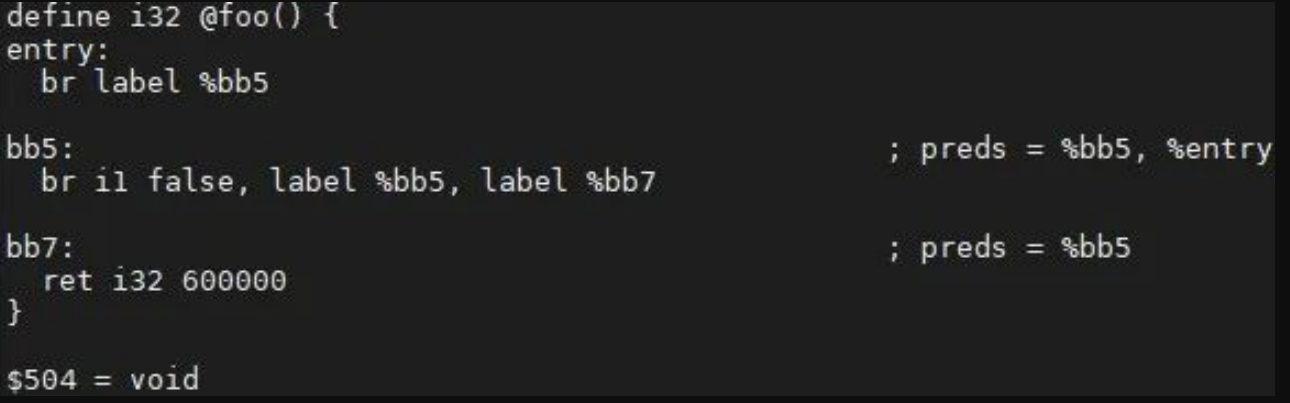
Step 3: Delete all dead instructions and check whether their operands need to be deleted. In the example, %tmp4, as the operand of %0, has a user %x.03.0, so it cannot be considered as a dead instruction to be deleted. The optimization results are as follows:
References
- https://llvm.org/docs/LoopTerminology.html
- Compilers: Principles, Techniques, & Tools by Alfred V. Aho (Author), Monica S. Lam (Author), Ravi Sethi (Author)
- BiSheng Compiler: https://www.hikunpeng.com/developer/devkit/compiler/bisheng
- Original text: https://mp.weixin.qq.com/s/9CQheIx4nlPfp-xPff5PJQ
Welcome to join the Compiler SIG to communicate about compilation technologies. Scan the QR code to add the assistant WeChat to invite you.